Multilevel Algorithms for Inverse Problems with Elliptic PDE Constraints

We formulate a novel multilevel algorithm for the solution of Tikhonov-regularized first-kind Fredholm equations. An example is the source identification problem, in which the forward problem is an elliptic partial differential equation. Our method assumes the availability of an approximate Hessian operator for which, first, the spectral decomposition is known, and second, there exists a fast algorithm that can perform the spectral transform. Based on this decomposition we propose a Conjugate Gradients (CG) solver which we precondition with a multilevel subspace projection scheme. Our novel preconditioner significantly improves the performance of CG. Not only do we obtain mesh-independent performance, but also very good scalability in the case of small regularization parameter.

Fast Inversion Schemes for Diffuse Optical Tomography

We consider a problem where a scattering medium is excited by numerous light sources at the boundary. We would like to identify the absorption coefficient of the medium from given large number of boundary measurements. An example of this problem is diffuse optical tomography. We work out the precise analytical structure of the problem in the case of constant background coefficient and devise a fast inversion scheme that allows us to infer the absorption coefficient. Our current work is on taking advantage of this scheme to implement an efficient algorithm that works for nonconstant background coefficient as well.

Vesicles

Vesicles are locally-inextensible closed membranes that possess tension and bending energies. Vesicle flows model numerous biophysical phenomena that involve deforming particles interacting with a Stokesian fluid. For instance, they are used to model red blood cell motion and the transport of drug-carrying capsules. The goal of this project is to devise efficient numerical schemes to simulate such flows. While conventional techniques can be used to simulate isolated vesicles, new approaches are needed for large number of interacting vesicles. Integral equation methods are attractive for these problems as they avoid the need for volume mesh generation and re-meshing. They lead to a system of nonlinear integro-differential equations whose unknowns reside on the fluid-vesicle interfaces. We have developed a novel numerical scheme for such equations. It incorporates a new time- stepping scheme that allows much larger time-steps than the existing explicit schemes. The associated linear systems are solved in optimal time using spectral preconditioners, FFTs and the fast multipole method.

Parallel Octree Algorithms for Finite Element Applications

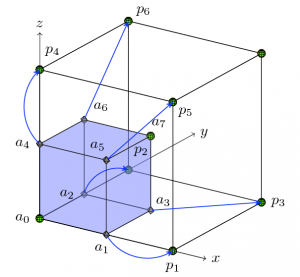    The primary focus of this project is developing scalable, fast, parallel algorithms for the numerical solution of elliptic and parabolic partial differential equations using the finite element method. Such equations are used to model the steady state and transient behaviors of numerous physical and biological processes. Heat conduction, Diffusive Material transport, Electrostatic potential distribution around a charge distribution, Protein folding and binding, Cancer growth and Cardiac electrophysiology are few such applications. Some of the applications involve complex geometries and non-uniform material properties. Some others model dynamic processes in which the geometry changes constantly. These dynamic processes are modeled as a sequence of static processes using some discretization of time. Hence these equations have to be solved a large number of times, at least once for each time step and sometimes more for more accurate schemes. For inverse-problem applications these equations need to be solved every optimization iteration. Hence, it is very important to be able to solve these equations as fast as possible. In order to be able to solve large dimensional problems efficiently, we have developed many novel scalable parallel algorithmic components like adaptive octree meshes and matrix-free multigrid pre-conditioned Krylov solvers for finite element discretizations on these meshes. Although parallel finite element solvers on adaptive meshes are available, they are bulky, slow and do not scale well. In contrast, the in-house parallel octree meshing tool, "DENDRO", which we developed, demonstrates excellent scalability and the cost of the finite element simulations using it are comparable to those using regular grids with the same number of elements. In practice, the number of elements in an adaptive mesh will be much less than that of a regular grid and hence we expect tremendous advantages over other existing methods especially for applications involving frequent re-meshing.

Multigrid Algorithms for Inverse Problems with Linear Parabolic PDE Constraints

We proposed a multigrid algorithm to solve distributed parameter identification problem with linear parabolic PDE constraints. We formulate the problem as a PDE constrained optimization problem with L2 Tikhonov regularization. We consider the problems in which the inversion variable is a function of space only. The main feature of our algorithm is that it is mesh-independent and inde- pendent of the regularized parameter. This makes the method algorithmically robust to the value of the regularization parameter and useful in cases where we require high-fidelity reconstruction. Multigrid algorithms have been mainly developed to solve linear system of equations which arise from the discretization of elliptic and parabolic PDEs. Smoothers like Jacobi, Gauss-Seidel, and CG, which work in the case of these PDEs do not work for inverse problems because of the different eigen-structure of the reduced Hessian operator. The main features of the proposed algorithm are: (1) an approximate reduced Hessian that is a composition of spectral filtering with an approximate reduced Hessian operator (based on inexact forward and adjoint solves); and (2) a smoothing scheme that uses a stationary second-order method that uses estimates of the high-frequency spectrum. It is crucial that the effectiveness of the smoother in the high-frequency regime is mesh independent; our methods fulfill this requirement. The multigrid scheme (a V-cycle) can be used as solver or as a preconditioner for a Krylov iterative method.

Funding